Calculadora: distância por triangulação.

Entre com, separados por ponto e vírgula ";", um valor para $\alpha$, um valor para $\beta$, um valor para $d$, e um valor para $x$.

Exemplo:

Input: "pi/6; pi/3; 1; sqrt(3)/2".

Output: aproximadamente "0.6751084105090466".




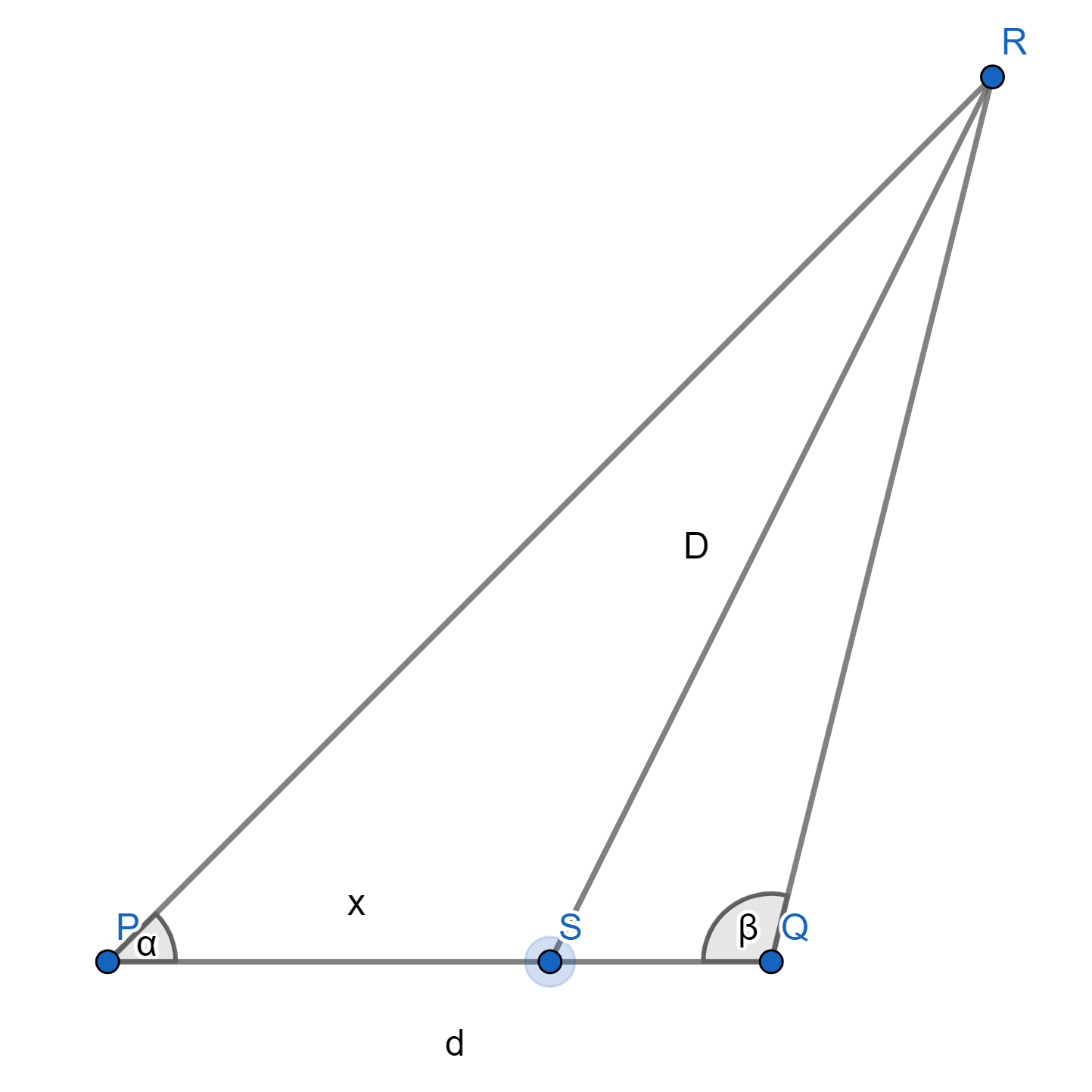
Distância de $S$ a $R$:

Distância por triangulação.

Sejam $\alpha$ o primeiro ângulo, $\beta$ o segundo ângulo, $d$ a distância entre os pontos $P$ e $Q$, $x$ o deslocamento na reta $\overleftrightarrow{PQ}$. Encontremos a distância $D$ entre $R$ e o ponto $S$ no segmento $\overline{PQ}$.

$m\left(\overline{QR}\right) = m\left(\overline{PR}\right) \cdot \dfrac{\sin \alpha}{\sin \beta}$

${\scriptsize \left[m\left({\overline{PR}}\right)\right]^2 + x^2 - 2x \cdot \left[m\left({\overline{PR}}\right)\right]\cos \alpha = \left[m\left({\overline{PR}}\right)\right]^2 \cdot \left(\dfrac{\sin \alpha}{\sin \beta}\right)^2 + (d - x)^2 - 2(d - x)\left[m\left({\overline{PR}}\right)\right] \cdot \left(\dfrac{\sin \alpha}{\sin \beta}\right)\cos \beta}$

Utilizando um software CAS, encontramos um $m\left({\overline{PR}}\right)$ positivo.

$\fbox{$D = \sqrt{\left[m\left({\overline{PR}}\right)\right]^2 + x^2 - 2x\left[m\left({\overline{PR}}\right)\right]\cos \alpha}$}$

Meme: o livro ordenando demonstrar.

 

Se $S_i$ gera $W_i$, $i \in \mathbb{N}_n$, mostre que $\displaystyle\bigcup_{i=1}^n S_i$ gera $\displaystyle\sum_{i=1}^n W_i$.

$S_1$ gera $W_1$. ${\large (I)}$

Vamos supor que $\displaystyle\bigcup_{i=1}^p S_i$ gera $\displaystyle\sum_{i=1}^p W_i$, $p < n$, mostremos que $\displaystyle\bigcup_{i=1}^{p+1} S_i$ gera $\displaystyle\sum_{i=1}^{p+1} W_i$

Seja $w$ um elemento de $\displaystyle\sum_{i=1}^p W_i$.

Se $w'$ é um elemento de $W_{p+1}$, $w + w'$ é um elemento de $\displaystyle\sum_{i=1}^{p+1} W_i$.

$w + w'$ é uma combinação linear de $\displaystyle\bigcup_{i=1}^p S_i$ e $S_{p+1}$, logo combinação linear de $\displaystyle\bigcup_{i=1}^{p+1} S_i$. ${\large (II)}$

Com ${\large (I)}$ e ${\large (II)}$, por indução finita, provamos.

Quod Erat Demonstrandum.

Coeficiente para sistema possível.

O sistema $\begin{cases}(\lambda + 1)x + y = 0\\ x + \lambda y = -2\end{cases}$ tem solução para $y = 0$. Qual o valor de $\lambda$?

Se $y = 0$, $x = -2$. Assim $-2\lambda - 2 = 0\ \Rightarrow\ \fbox{$\lambda = -1$}$.

Probabilidade de, em um hexágono, escolher um triângulo equilátero.

Aleatoriamente escolhem-se $3$ dos $6$ vértices de um hexágono regular. Qual a probabilidade dos vértices escolhidos formarem um triângulo equilátero?

$n(U) = \displaystyle{6 \choose 3} = 20$

Seja $A$ o evento dos vértices formarem um triângulo equilátero.

$n(A) = 2$

$P(A) = \dfrac{2}{20} = 10\%$

Sejam $W_1, \dots , W_n$ subespaços, mostre que $L(W_1, \dots , W_n) = W_1 + \dots + W_n$.

Definamos $L(W_1, \dots , W_n) = L(W_1 + \dots + W_n)$.

Obviamente $W_1 + \dots + W_n \subset L(W_1, \dots , W_n)$. ${\large (I)}$

Sejam $w$ um elemento de $L(W_1, \dots , W_n)$, e $a_i,\ i \in \mathbb{N}_m$ escalares,

$w = \displaystyle\sum_i a_i \displaystyle\sum_{j=1}^n w_j = \displaystyle\sum_{j=1}^n w_j \displaystyle\sum_i a_i,\ w_j \in W_j$.

Tomando quaisquer $a_i$'s tais que $\displaystyle\sum_i a_i = 1$, $w = \displaystyle\sum_{j=1}^n w_j$ que é um elemento de $\displaystyle\sum_{j=1}^n W_j$. Logo $L(W_1, \dots , W_n) \subset W_1 + \dots + W_n$. ${\large (II)}$

${\large (I)}\ \wedge\ {\large (II)}\ \Rightarrow\ L(W_1, \dots , W_n) = W_1 + \dots + W_n$

Quod Erat Demonstrandum.

Seja $S$ um subconjunto de um espaço vetorial $V$. Mostre que $V + S = V$.

$V + S = \{v + s\ :\ v \in V\ \wedge\ s \in S\}$

Mas $s \in V$ e, se $s_1 \in V$ e $s_2 \in V$, $s_1 + s_2 \in V$.

Quod Erat Demonstrandum.

Corolário: se $W$ é espaço vetorial, $W + W = W$.

Sejam $A$ e $B$ matrizes para as quais $AB$ está definido. Mostrar que o espaço de colunas de $AB$ está contido no espaço de colunas de $A$.

Basta mostrar que uma combinação linear das colunas de $AB$ é uma combinação linear das colunas de $A$.

Sejam $a_{ij}$ um elemento de $A$, $b_{jk}$ um elemento de $B$, $\alpha_k,\ k = 1,\dots ,o$ escalares, e $c_i$ uma combinação linear das colunas de $AB$ na linha $i$:

$c_i = \displaystyle\sum_{k=1}^o \alpha_k \displaystyle\sum_{j=1}^n a_{ij}b_{jk} = \displaystyle\sum_{j=1}^n a_{ij} \displaystyle\sum_{k=1}^o \alpha_k b_{jk}$.

Ou seja, $c_i$ é uma combinação linear das colunas de $A$ na linha $i$.

Quod Erat Demonstrandum.

Largura de uma calçada em torno de um jardim.

Um pedreiro demora um certo tempo para construir um jardim circular de raio $10\ m$. Em volta do jardim demora um tempo $44 \%$ menor para construir uma calçada circular em torno do jardim. Se o tempo de construção for diretamente proporcional à área a construir, determinar a largura da calçada.

O jardim tem $100\pi$ de área. Sendo $\ell$ a largura procurada, a calçada terá uma área de $(10 + \ell)^2 \pi - 100\pi$.

Se o tempo de construção da calçada foi $0,56$ do tempo de construção do jardim:

$(10 + \ell)^2 \pi - 100\pi = 56\pi\ \Rightarrow\ \ell^2 + 20\ell - 56 = 0\ \Rightarrow\ \fbox{$\ell = 2\sqrt{39} - 10$}$.

Mostre que $L(L(S)) = L(S)$.

Sejam $s$ um elemento de $L(L(S))$, $s_i,\ i \in \mathbb{N}$ elementos de $S$, $a_i,\ i \in \mathbb{N}$ escalares e $b_j,\ j \in \mathbb{N}$ escalares.

Obviamente $L(S) \subset L(L(S))$. ${\large (I)}$

$s = \displaystyle\sum b_j\displaystyle\sum a_i s_i = \displaystyle\sum_i \left(\displaystyle\sum_j b_j a_i\right)s_i$, que é um elemento de $L(S)$. Assim, $L(L(S)) \subset L(S)$. ${\large (II)}$

${\large (I)}\ \wedge\ {\large (II)}\ \Rightarrow\ L(L(S)) = L(S)$

Quod Erat Demonstrandum.

Meme: escrever Matemática.

 

Mostre que, se $S \subset T$, $L(S) \subset L(T)$.

Sejam $t$ um elemento de $L(T)$, $t_i\ i \in \mathbb{N}$ elementos de $T$, e $a_i,\ i \in \mathbb{N}$ escalares.

$t = \displaystyle\sum a_it_i$

Fazendo $a_k = 0$ para $t_k \in T - S$, $t$ é um elemento de $L(S)$.

Quod Erat Demonstrandum.

Mostre que $L(S) = L(S \cup \{O\})$.

Sejam $s$ um elemento de $L(S)$, $s'$ um elemento de $L(S \cup \{O\})$, $s_i,\ i \in \mathbb{N}$ elementos de $S$, e $a_i,\ i \in \mathbb{N}$ e $b$ escalares.

$s = \displaystyle\sum a_is_i = \left(\displaystyle\sum a_is_i\right) + bO$ que é um elemento de $L(S \cup \{O\})$. Assim $L(S) \subset L(S \cup \{O\})$. ${\large (I)}$

$s' = \left(\displaystyle\sum a_is_i\right) + bO= \displaystyle\sum a_is_i$ que é um elemento de $L(S)$. Assim $L(S \cup \{O\}) \subset L(S)$. ${\large (II)}$

${\large (I)}\ \wedge\ {\large (II)}\ \Rightarrow\ L(S) = L(S \cup \{O\})$

Quod Erat Demonstrandum.

Calculadora: dia da semana.

Entre com, separados por barra "/", a data do dia, a data do mês, e o ano:

Exemplo:

Input: "8 / 2 / 2022".
Output: "Terça-feira.".




Dia da semana:

Uma elipsoide de revolução.

Obter as equações paramétricas da superfície resultante da rotação da elipse: $\begin{cases}x = 0\\ y = 3\cos u\\ z = 2\sin u\end{cases}, u \in [0, 2\pi[$, em torno do eixo $Oy$.

$\begin{cases}x = 2(\sin u)(\sin v)\\ y = 3\cos u\\ z = 2(\sin u)(\cos v)\end{cases}, u \in [0, 2\pi[, v \in [0, \pi[$.

Demonstre: $L(S)$ é a intersecção de todos os subespaços de $V$ que contém $S$.

Seja $U$ tal intersecção.

Se $S$ é subespaço, $U = S$. ${\large (I)}$

Se $S$ não é subespaço, $U = L(S)$. ${\large (II)}$

${\large (I)}\ \wedge\ {\large (II)}\ \Rightarrow\ U \subset L(S)$ ${\large (III)}$

Seja $s'$ um elemento de $L(S)$ que não pertence a $U$, no entanto, como $U$ é subespaço, $s'$ pode ser obtido como uma combinação linear dos elementos de $S$, e, consequentemente, dos elementos de $U$. Onde temos uma contradição. Logo:

$L(S) \subset U$. ${\large (IV)}$

${\large (III)}\ \wedge\ {\large (IV)}\ \Rightarrow\ L(S) = U$

Quod Erat Demonstrandum.

Determinar um vetor do $\mathbb{R}^3$ que gera a intersecção dos subespaços $U$ e $V$, sendo $U$ o plano $xy$ e $V$ o espaço gerado por $(1, 2, 3)$ e $(1, -1, 1)$.

Seja $v = a(1, 2, 3) + b(1, -1, 1) = (a + b, 2a - b, 3a + b)$ um vetor de $V$.

Fazendo $3a + b = 0$, temos como intersecção de $U$ e $V$ $(-2a, 5a, 0)$.

Assim, $(-2, 5, 0)$ é um vetor que gera $U \cap V$.

Utilizando o algoritmo de Briot-Ruffini, dividir $x^3 - 2x^2 + 3x - 1$ por $2x - 4$.

Sejam $Q(x)$ o polinômio quociente e $R(x)$ o polinômio resto.

$x^3 - 2x^2 + 3x - 1 = \underset{q(x)}{\underbrace{2Q(x)}}(x - 2) + R(x)$

$\begin{array}{l | l}2 & \begin{matrix} 1 & -2 & 3 & -1\end{matrix}\\ \hline\\ & \begin{matrix}1 & 0 & 3 & 5\end{matrix}\end{array}$

Logo $Q(x) = \dfrac{q(x)}{2} = \dfrac{x^2}{2} + \dfrac{3}{2}$ e $R(x) = 5$.

Quais os valores máximo e mínimo da função: $f(x) = \left(\dfrac{1}{2}\right)^{4x - x^2}$?

O expoente não tem mínimo, e, como a base está entre $0$ e $1$, a função não tem máximo.

O máximo do expoente é $4$, logo o mínimo valor de $f$ é $\dfrac{1}{16}$.

Qual o valor de $\cos 22,5^o + \sin 22,5^o$?

$\cos \dfrac{\pi}{8} + \sin \dfrac{\pi}{8} = \cos \dfrac{\pi}{8} + \cos \dfrac{3\pi}{8} = 2\left(\cos \dfrac{\pi}{4}\right)\left(\cos \dfrac{\pi}{8}\right) = $

$= \sqrt{2}\sqrt{\dfrac{1 + \cos \dfrac{\pi}{4}}{2}} = \fbox{$\sqrt{1 + \dfrac{\sqrt{2}}{2}}$}$

Se $0,6 \%$ de $3\dfrac{1}{3} = 3x - 1$, qual o valor de $x$?

$\dfrac{\cancelto{1}{6}}{\bcancelto{50}{300}} = 3x - 1\ \Rightarrow\ 51 = 150x\ \Rightarrow\ \fbox{$x = \dfrac{51}{150}$}$

Resolver a equação $\log_3 x + \log_3 x^4 + \log_3 x^7 + \dots + \log_3 x^{25} = 234$.

Observemos que o primeiro membro é uma PA. Para sabermos o número de termos, resolvamos a equação:

$25 = 1 + (n - 1) \cdot 3\ \Rightarrow\ n = 9$.

Calculemos agora a soma dos termos de tal PA:

$\dfrac{(\log_3 x + 25\log_3 x) \cdot 9}{2} = 117\log_3 x$.

Logo $\log_3 x = 2\ \Rightarrow\ \fbox{$S = \{9\}$}$.

Mostre que os complexos $w = 2 + 3i$ e $z = 1 - 2i$ geram o corpo $\mathbb{C}$ como espaço vetorial sobre o corpo $\mathbb{R}$.

Basta mostrar que existem escalares $x$ e $y$ tais que $xw + yz = a + bi,\ a,b \in \mathbb{R}$, ou seja:

$\begin{cases}2x + y = a\\ 3x - 2y = b\end{cases}$, donde $x = \dfrac{2a + b}{7}$ e $y = \dfrac{3a - 2b}{7}$.

Quod Erat Demonstandum.

Mostre que os polinômios $(1 - t)^3$, $(1 - t)^2$, $1 - t$ e $1$ geram os polinômios de grau menor ou igual a $3$.

Basta mostrar que todo polinômio $at^3 + bt^2 + ct + d$ é uma combinação linear de $(1 - t)^3$, $(1 - t)^2$, $1 - t$ e $1$, ou seja, que existem escalares $x$, $y$, $z$ e $w$ tais que, para todos $a$, $b$, $c$ e $d$:

$x(1 - t)^3 + y(1 - t)^2 + z(1 - t) + w = at^3 + bt^2 + ct + d$.

Desenvolvendo:

$-xt^3 + (3x + y)t^2 + (-3x - 2y - z)t + (x + y + z + w) = at^3 + bt^2 + ct + d$.

Donde concluímos que existem:

$x = -a$, $y = b + 3a$, $z = -3a - 2b - c$ e $w = a + b + c + d$.

Quod Erat Demonstrandum.

Resolver em $\mathbb{R}$: $3^{x + 2} + 9^{x - 1} = 90$.

$3^{x + 2} + 3^{2x - 2} = 90\ \Rightarrow\ 9 \cdot 3^x + \dfrac{3^{2x}}{9} = 90$

Seja $y = 3^x$:

$y^2 + 81y - 810 = 0\ \Rightarrow\ y = -90\ \vee\ y = 9\ \Rightarrow\ x = 2$.

$\fbox{$S = \{2\}$}$

Em um exame, há um total de $50$ questões com $5$ alternativas cada, sendo apenas $1$ correta. Marcando as questões aleatoriamente, qual a probabilidade de um concursando acertar $60 \%$ da prova?

Trata-se um experimento binomial.

$P = \displaystyle{50 \choose 30} \left(\dfrac{1}{5}\right)^{30}\left(\dfrac{4}{5}\right)^{20} \approx 00000000,6 \%$

Encontrar a área finita compreendida entre os gráficos de $y =x^2$ e $y = x$.

As intersecções entre os gráficos são $(0, 0)$ e $(1, 1)$, logo, chamando tal área de $A$:

$A\ =\ \displaystyle\int_0^1 x - x^2\ dx\ =\ \left.\left(\dfrac{x^2}{2} - \dfrac{x^3}{3}\right)\right|_0^1 = \dfrac{1}{2} - \dfrac{1}{3} =\ \fbox{$\dfrac{1}{6}$}$.

Utilizando a Regra de Chió, encontrar o determinante de $\begin{bmatrix}3 & 4\\ -1 & 5\end{bmatrix}$.

$\begin{vmatrix}3 & 4\\ -1 & 5\end{vmatrix} = 3\begin{vmatrix}1 & \dfrac{4}{3}\\ -1 & 5\end{vmatrix} = 3\begin{vmatrix}5 + \dfrac{4}{3}\end{vmatrix} = 3\begin{vmatrix}\dfrac{19}{3}\end{vmatrix} = 19$

Meme: sabe Matemática, LaTeX e programação.

 

Encontrar $\displaystyle\int \sin^3 x\ dx$.

$I\ =\ \displaystyle\int \sin^3 x\ dx\ =\ \displaystyle\int (\sin x)(1 - \cos^2 x) x\ dx\ =$

$=\ -(\cos x)(1 - \cos^2 x) + 2\displaystyle\int (\cos^2 x)(\sin x)\ dx\ =$

$=\ -\cos x + \cos^3 x + 2\displaystyle\int (1 - \sin^2 x)(\sin x)\ dx\ =$

$=\ -\cos x + \cos^3 x + 2\displaystyle\int \sin x\ dx - 2\underset{I}{\underbrace{\displaystyle\int\sin^3 x\ dx}}$

$\fbox{$\displaystyle\int \sin^3 x\ dx\ =\ \dfrac{\cos^3 x}{3} - \cos x + c$}$

Simplificar $\cos^4 x - \sin^4 x$.

$\cos^4 x - \sin^4 x = \underset{1}{\underbrace{(\cos^2 x + \sin^2 x)}}(\cos^2 x - \sin^2 x) = \cos 2x$