 |
Observe o triângulo acutângulo abaixo e determine o comprimento do lado $AC$ e o ângulo formado no vértice $A$.
$b^2 = 100 + 64 - 160\cos 50^\text{o}\ \Rightarrow\ b = 2\sqrt{41 - 40\cos 50^\text{o}} \approx\ \fbox{$7,8$}$
$\dfrac{\sin 50^\text{o}}{2\sqrt{41 - 40\cos 50^\text{o}}} = \dfrac{\sin \hat{A}}{8}\ \Rightarrow\ \hat{A} = \arcsin \dfrac{4\sin 50^\text{o}}{\sqrt{41 - 40\cos 50^\text{o}}} \approx\ \fbox{$51,6^\text{o}$}$
Pedro, localizado a 8 metros do chão, está observando o prédio vizinho. Sabendo que a sua distância para o prédio vizinho é de 8 m e entre as duas estruturas forma-se um triângulo, cujo ângulo ABC é de 105º, determine a altura do prédio que Pedro está observando.
$h = 8 + 8\tan (105^\text{o} - 45^\text{o}) = 8 + 8\sqrt{3} = \fbox{$8(1 + \sqrt{3})\ \text{m}$}$
João trabalha em um prédio e todos os dias tem que subir uma escada de 8 degraus, que tem aproximadamente 2 metros de comprimento e 30 graus de inclinação. De acordo com a figura a seguir, determine a altura de cada degrau.
$8h = 2\sin \dfrac{\pi}{6} = 1\ \therefore\ h = 0,125 \text{m} = \fbox{$12,5 \text{cm}$}$
Encontrar o valor de $x$.
$x = \dfrac{3\ \text{cm}}{\cos 30^o} = \fbox{$2\sqrt{3}\ \text{cm}$}$
| A equação aparecerá aqui... |
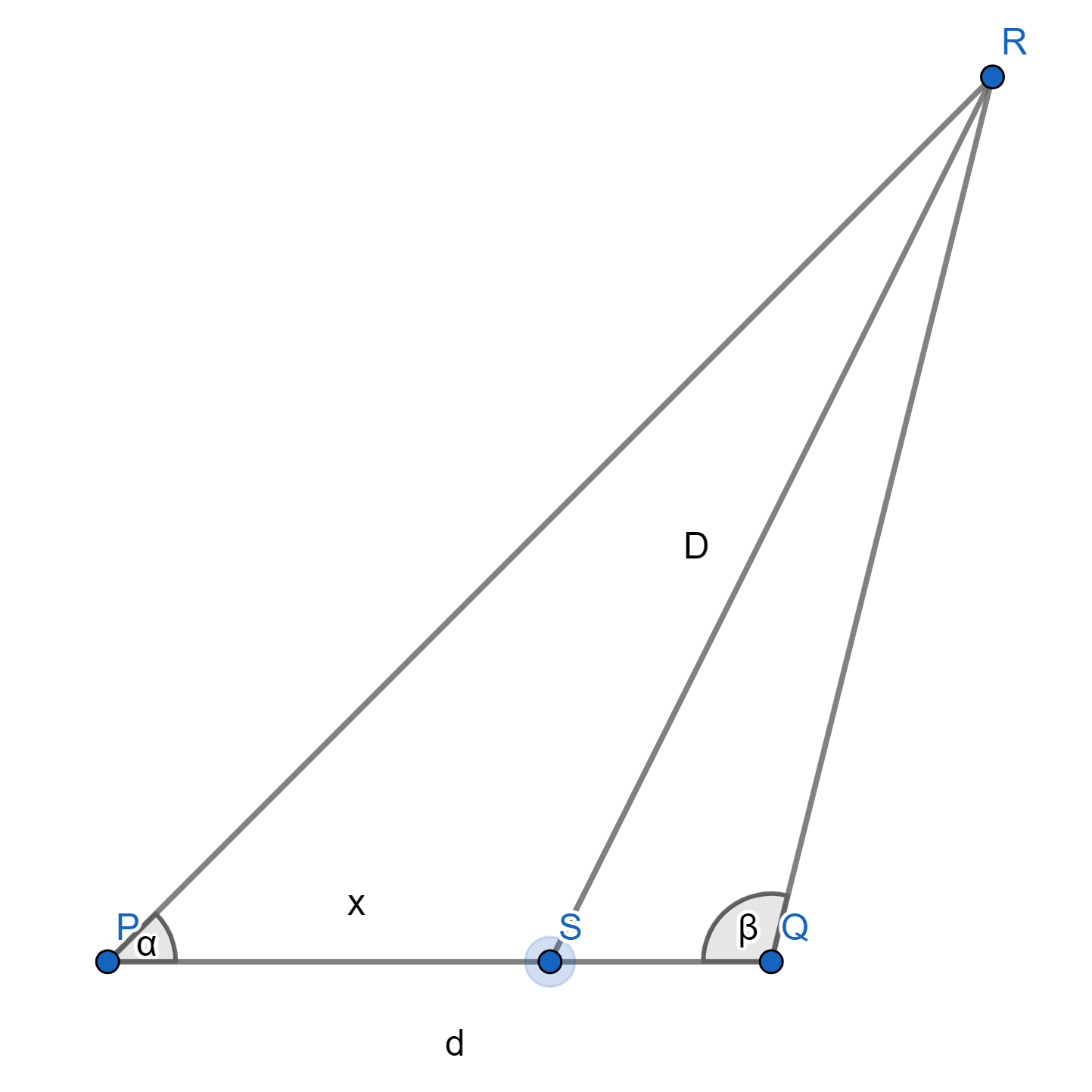
Sejam $\alpha$ o primeiro ângulo, $\beta$ o segundo ângulo, $d$ a distância entre os pontos $P$ e $Q$, $x$ o deslocamento na reta $\overleftrightarrow{PQ}$. Encontremos a distância $D$ entre $R$ e o ponto $S$ no segmento $\overline{PQ}$.
$m\left(\overline{QR}\right) = m\left(\overline{PR}\right) \cdot \dfrac{\sin \alpha}{\sin \beta}$
${\scriptsize \left[m\left({\overline{PR}}\right)\right]^2 + x^2 - 2x \cdot \left[m\left({\overline{PR}}\right)\right]\cos \alpha = \left[m\left({\overline{PR}}\right)\right]^2 \cdot \left(\dfrac{\sin \alpha}{\sin \beta}\right)^2 + (d - x)^2 - 2(d - x)\left[m\left({\overline{PR}}\right)\right] \cdot \left(\dfrac{\sin \alpha}{\sin \beta}\right)\cos \beta}$
Utilizando um software CAS, encontramos um $m\left({\overline{PR}}\right)$ positivo.
$\fbox{$D = \sqrt{\left[m\left({\overline{PR}}\right)\right]^2 + x^2 - 2x\left[m\left({\overline{PR}}\right)\right]\cos \alpha}$}$
Aleatoriamente escolhem-se $3$ dos $6$ vértices de um hexágono regular. Qual a probabilidade dos vértices escolhidos formarem um triângulo equilátero?
$n(U) = \displaystyle{6 \choose 3} = 20$
Seja $A$ o evento dos vértices formarem um triângulo equilátero.
$n(A) = 2$
$P(A) = \dfrac{2}{20} = 10\%$
Um pedreiro demora um certo tempo para construir um jardim circular de raio $10\ m$. Em volta do jardim demora um tempo $44 \%$ menor para construir uma calçada circular em torno do jardim. Se o tempo de construção for diretamente proporcional à área a construir, determinar a largura da calçada.
O jardim tem $100\pi$ de área. Sendo $\ell$ a largura procurada, a calçada terá uma área de $(10 + \ell)^2 \pi - 100\pi$.
Se o tempo de construção da calçada foi $0,56$ do tempo de construção do jardim:
$(10 + \ell)^2 \pi - 100\pi = 56\pi\ \Rightarrow\ \ell^2 + 20\ell - 56 = 0\ \Rightarrow\ \fbox{$\ell = 2\sqrt{39} - 10$}$.
$r = \dfrac{g}{2} = 3\sqrt{3}$, $h = \dfrac{\sqrt{3}}{2} \cdot g = 9$.
$V = \dfrac{\pi r^2 h}{3} = \dfrac{243\pi }{3} = \fbox{$81\pi$}$
$\dfrac{a}{3} = -\dfrac{10}{6}\ \Rightarrow\ \fbox{$a = -5$}$
Seja $\theta$ o ângulo adjacente aos lados de medida $5$ e $8$:
$49 = 25 + 64 - 80\cos \theta\ \therefore\ \theta = \arccos \dfrac{1}{2}$.
Seja $m$ a medida da mediana relativa ao maior lado:
$m^2 = 25 + 16 - 40 \cdot \dfrac{1}{2}\ \therefore\ \fbox{$m = \sqrt{21}\ cm$}$.
